Intro
In my opinion, there should always be a balance of chance in sports, especially in the playoffs. The better team should win more often, but there should always lurk the possibility of a thrilling upset. Put to the extreme, skill has no meaning if the better team wins as often as they lose; and if the better team always wins, then there is no fun at all in the game.
In this vein, playing to a higher point total causes the better team will win more often. If this isn't intuitively obvious to you, consider the following examples.
- Is a pickup team more likely to beat 2016 Revolver in a game to 1 or a game to 15?
- Are the 2012 Charlotte Bobcats more likely to beat the 1996 Chicago Bulls in a single game or in a 7-game series?
This relationship between variance and game length is true in less extreme examples, too - for instance, between two relatively evenly matched teams in the quarterfinals of club nationals, playing to 15.
In this blog post, we'll explore how often the better team wins in big ultimate games, and how much changing the score total changes the likelihood that the better team wins.
Approach
We'll model the game as a series of independently points that can be won by either team [1]. Then, if team A has probability p of winning any given point in a game to n points, the probability that they win the game is
\(F1: \sum_{i = 0}^{n-1} \frac{(n+i-1)!}{(n-1)! i!} (1-p)^i p^n \)
We know that this is equal to the probability that team A beats team B, which we can calculate another way: from their elo rankings. That formula is
\( F2: \frac{1}{1 + 10^{\frac{elo_B - elo_A}{400}}} \)
With these two formulae, our approach becomes straightforward. From the USAU rankings, which give elo scores, we use F2 to calculate the expected chance of the better team winning. From there, we can invert F2 [2] to find the probability that the better team wins any given point under the constraints of our model [3]. Then all we need to do is run that number back through F1 with various point totals and compare the outcomes.
Results
For our range of possible Elo differences, let's look at historical data. The biggest difference at club nationals in 2023 was between Scandal (2606.7) and Pop (1402.13), for a whopping difference of 1204.57 elo points [4]. We'll start with this large range - anywhere up to 1200 elo points differential - and range the possible point totals from 1 to 25. Here's what those results look like:
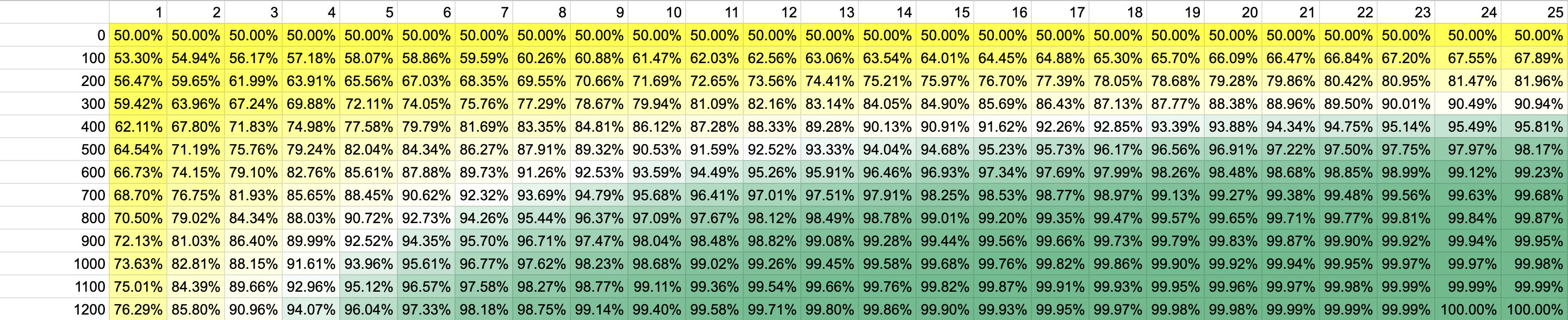
A few takeaways:
- In a game to 15, anywhere more than a 400 point elo difference gives you a >=90% chance of winning
- In a game to 25, a 300 point elo difference should give the same odds of winning (>=90%) to the better team
- Even in a game to 1, Scandal has a 75% chance of beating Pop
But we can look more fine-grained. We know games are played to odd numbers in the teens, so we'll examine odd scores from 11 to 21. Furthermore, the games we care most about occur in the bracket at USAU nationals. So let's look at how big the elo gap is for those games. Here's that histogram:
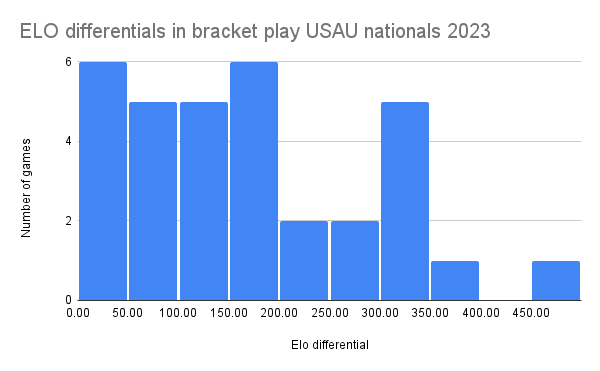
Most games in the bracket at nationals occur between teams that have less than or equal to about 300 elo points in ranking differential, with a somewhat flat distribution below that number. We'll accordingly restrict our examination window to below elo 300 points in ranking differential. Then, here's that data:
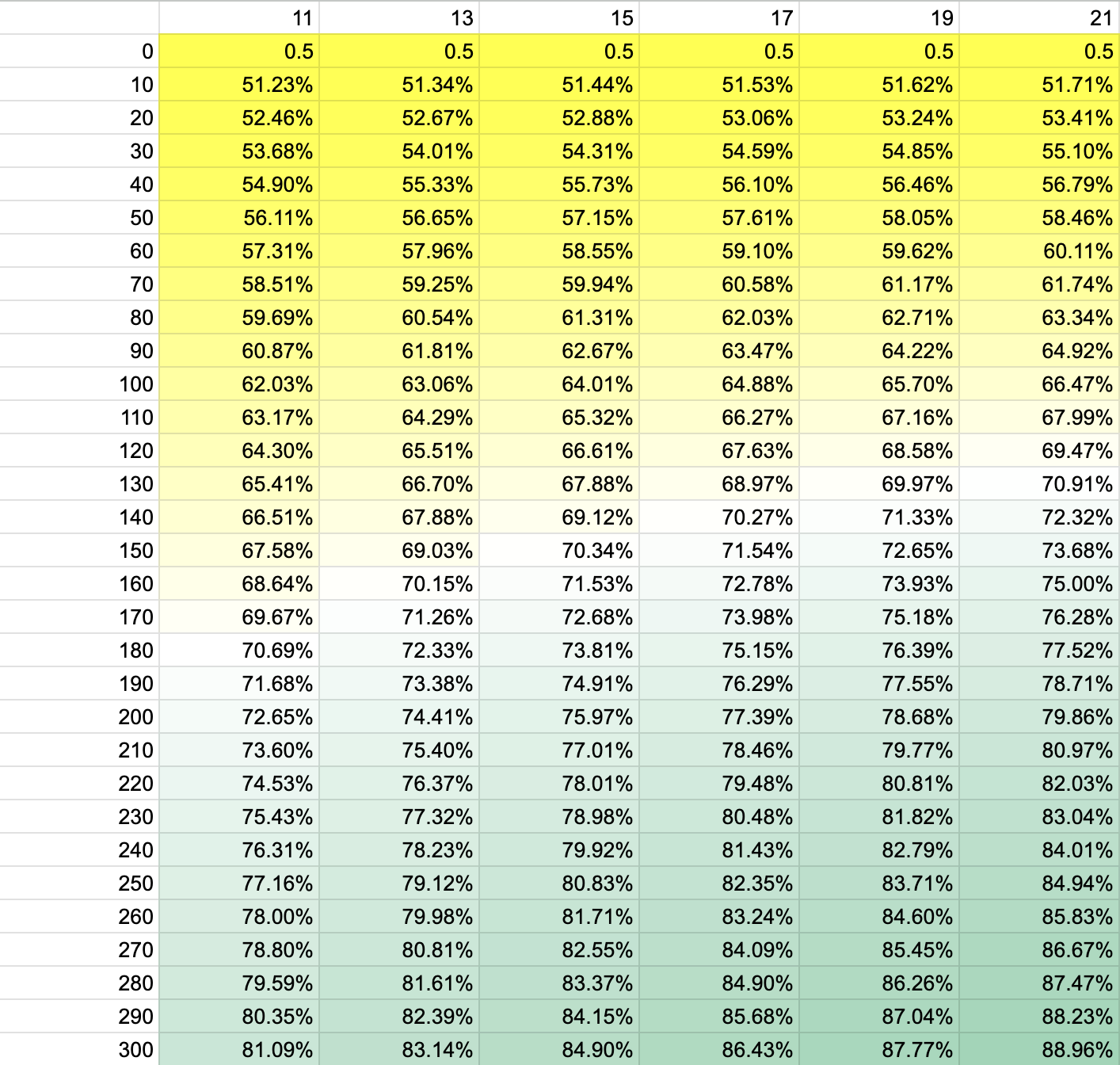
A few takeaways:
- Elo differential makes a much larger difference than point total
- We could play short games and be just fine - even in games to 11, the better team prevails nearly as often as they do in games to 15
Conclusion
The point total of a game affects the chance of the winning team less than I had anticipated. For example, in the men's final between Truck Stop (2499.23) and Machine (2189.71), increasing the game length from 15 to 19 only decreases Machine's chances by about four percent. In the more evenly matched semifinal between Hybrid (1823.85) and XIST (1920.86), increasing the game length to 19 only increases XIST's chances by about two and a half percent.
This blog post changed my mind. I came into writing it expecting it to be an argument for longer games from the standpoint of reducing volatility in winning. Now I see that the game length matters little, though there still is a huge amount of variance in the winners of nationals any way about it.
Resources
[1] this is a flawed model, since holds and breaks are obviously not independent. But it will suffice for our purposes.
[2] We can't invert a 15-degree polynomial directly but we can invert it programmatically quite easily.
[3] Another assumption is that the USAU rankings are meant to encode information about games to 15.
[4] This indicates that Pop has a 0.000000142% chance of winning any given game against Scandal, or 1.42 in 10 billion.
